Training AlphaZero with Monte Carlo Tree Search: Part 1

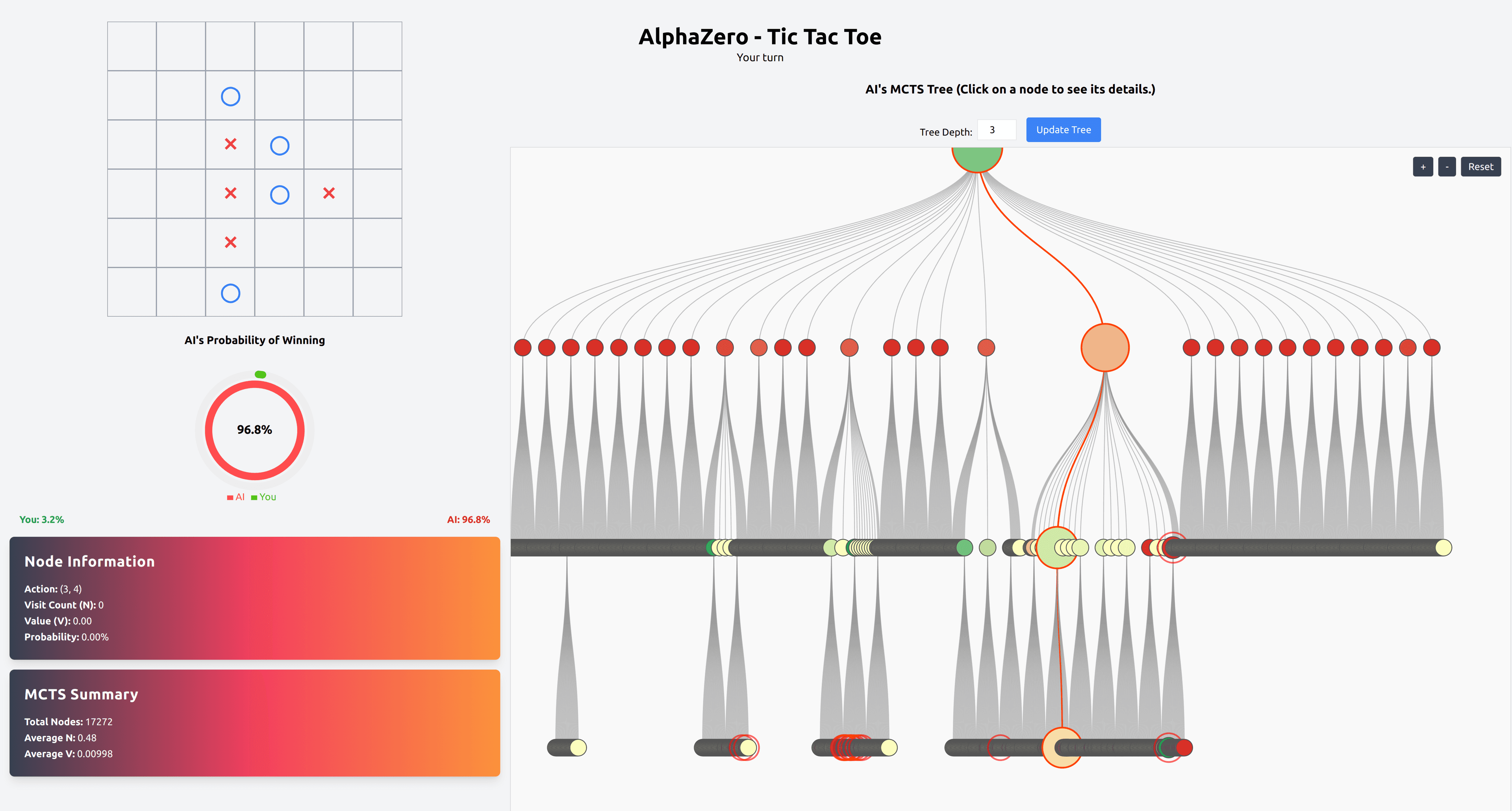
Table of Contents

1. Introduction

   • Brief overview of AlphaZero and its significance
   • Why Tic Tac Toe as a starting point?
   • Goals for the series

2. Understanding the Game Setup

   • Rules and mechanics of Tic Tac Toe
   • Overview of the ConnectN implementation
     • Winning conditions
     • Game states and moves
     • Key functions (e.g., get_lines, in_a_row)

3. What is Monte Carlo Tree Search (MCTS)?

   • Basics of MCTS
     • Exploration vs Exploitation trade-off
     • Role of UCB (Upper Confidence Bound)
   • How MCTS works step-by-step
   • Integration with AlphaZero

4. Building the Neural Network for AlphaZero

   • Overview of the Policy network architecture
     • Input representation (game state)
     • Action head (policy output)
     • Value head (game outcome prediction)
   • Code walkthrough of the Policy class

5. Training AlphaZero with MCTS

   • Explanation of the training loop
     • MCTS simulation for move selection
     • Backpropagation of values
     • Optimizing the policy network
   • Key parameters in training
     • Number of episodes
     • Exploration constants (e.g., c, Nmax)

6. Code Walkthrough of Monte Carlo Tree Search

   • Detailed explanation of the provided scripts:
     • MCTS.py: Monte Carlo Tree Search implementation

7. Evaluating the AlphaZero Agent

   • Metrics for evaluation
     • Win rate against random opponents
     • Training loss over episodes
   • Visualizing the gameplay (e.g., using matplotlib)
   • Saving and loading trained policies

8. Challenges and Considerations

   • Key challenges in implementing AlphaZero for Tic Tac Toe
   • Limitations of the current approach
   • Lessons learned during development

9. Conclusion and Next Steps

   • Recap of achievements in this part
   • Preview of the next blog (FastAPI backend)

Codes: Check the Github Repo for the full code

1. Introduction

The Story of Lee Sedol vs. AlphaGo

It was March 2016. The world watched in awe as Lee Sedol, a 9-dan professional Go player, faced off against AlphaGo, an AI developed by DeepMind. The game was Go—a complex board game with more possible moves than there are atoms in the universe. Lee Sedol, a legend in the field, was expected to dominate. But history had a different plan.

AlphaGo not only beat Lee but displayed a move so unconventional and brilliant that even seasoned players reevaluated their understanding of the game. That was the turning point—a moment when AI proved it could outthink humans in strategy games requiring intuition and foresight.

The Magic Behind AlphaZero

AlphaGo's triumph paved the way for AlphaZero, an even more advanced AI system. Unlike AlphaGo, which relied heavily on human expert knowledge, AlphaZero learned to dominate games like Chess, Shogi, and Go purely by playing against itself. It needed no human guidance, just the rules of the game. The secret? A combination of Monte Carlo Tree Search (MCTS) and Reinforcement Learning.

For more on AlphaZero's origins, you can explore DeepMind's research here.

Why Tic-Tac-Toe?

Now, you might wonder: why Tic-Tac-Toe? Isn't it too simple? Yes, Tic-Tac-Toe is a solved game, but it provides the perfect sandbox for experimenting with and understanding complex AI concepts like MCTS and AlphaZero-style training. By mastering Tic-Tac-Toe, we build a strong foundation to scale up to more complex games.

Also, we will play a 6 x 6 Tic-Tac-Toe instead of the traditional 3 x 3. In order to win this game, the player has to create four "X" or "O" in series instead of the traditional three.

This blog series will document the exciting journey of building an AlphaZero-inspired AI to dominate Tic-Tac-Toe, starting with training the model in Part 1.

---

Goals for the Series

By the end of this series, you'll not only understand how to build an AlphaZero-inspired agent but also how to bring it to life with a backend and frontend. Here's what we'll cover:

• Part 1: Training the model with MCTS
• Part 2: Developing a FastAPI backend for our AI
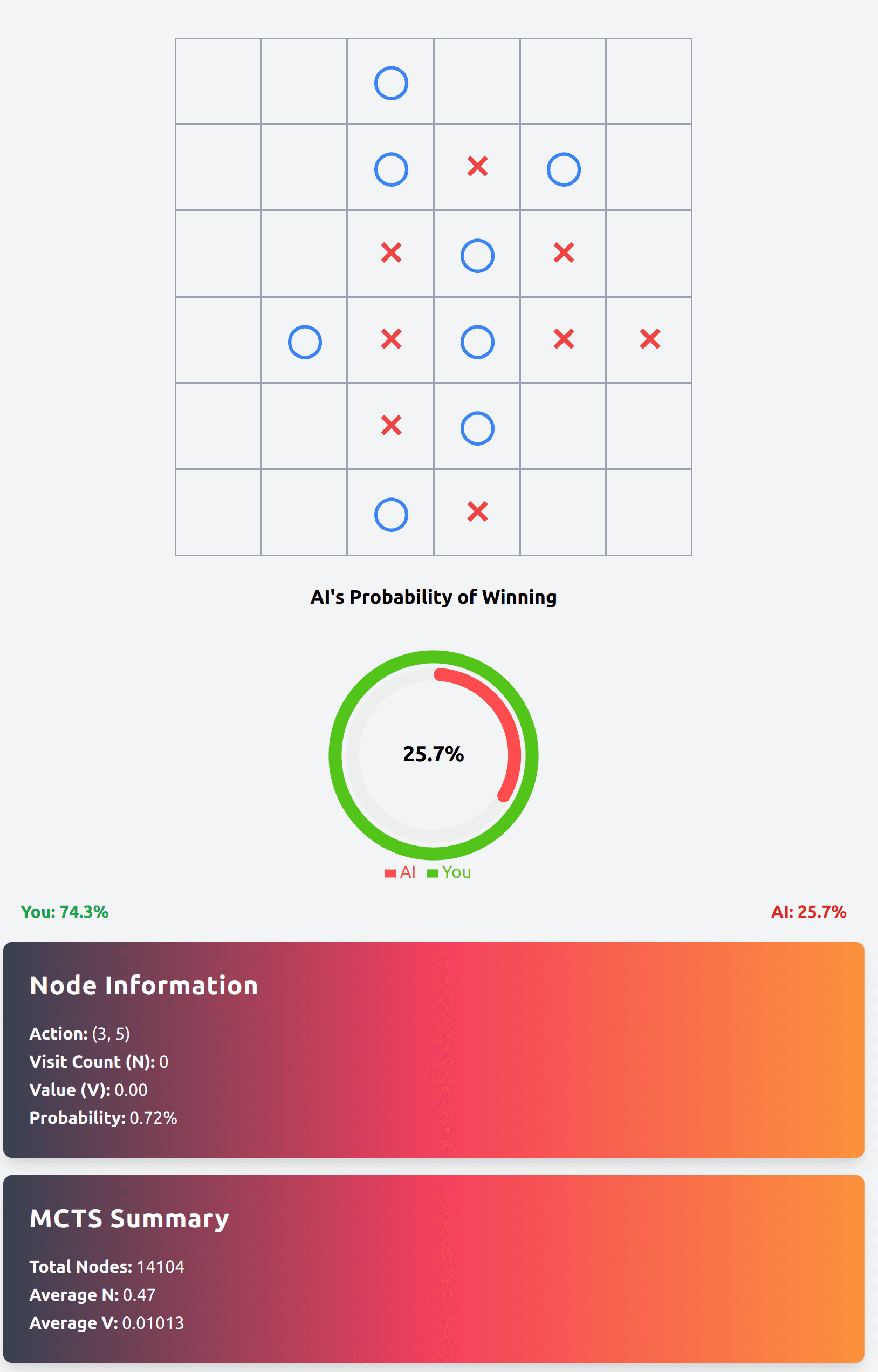
• Part 3: Creating a gorgeous, user-friendly frontend in React, where you will play live against a super-human agent. Here you will see live updates to the Game Tree driven by Monte Carlo Tree Search and the trained policy and also get the probability of win at each move.

In this part, we’ll lay the foundation, exploring AlphaZero's core mechanics, implementing the neural network, and training it with MCTS.

The full code can be found here.

Let’s dive in!

---

2. Understanding the Game Setup

Rules and Mechanics of Tic-Tac-Toe

Tic-Tac-Toe is a classic game where players take turns marking spaces on a grid, aiming to align their symbols in a row, column, or diagonal. The traditional game uses a 3 x 3 grid, but we're upping the ante with a 6 x 6 grid. In this expanded version, the goal is to align 4 "X" or "O" symbols in a row, making the game more challenging and interesting.

The larger grid and increased winning condition require more strategic planning, providing the perfect setup to train an AlphaZero-inspired AI. If you're unfamiliar with the standard game rules, check out a simple explanation of Tic-Tac-Toe here.

Overview of the ConnectN Implementation

To implement our custom Tic-Tac-Toe game, we’ve built a Python class called ConnectN. This class handles everything from maintaining the game state to determining the winner. Let’s break it down.

Winning Conditions

The objective in this 6 x 6 version is simple but challenging:

• Players must connect 4 consecutive symbols in a row, column, or diagonal.

• The game ends when a player wins or the board is fully occupied (resulting in a draw).

  

The logic to check winning conditions relies on the get_lines and in_a_row functions:

• get_lines(matrix, loc): Extracts rows, columns, and diagonals passing through a specific location on the grid.
• in_a_row(v, N, i): Checks if a vector contains N consecutive symbols for a given player.

Key Features of the ConnectN Class

1. Game State: The board is represented as a 2D NumPy array where:
   • 0 indicates an empty cell.
   • 1 represents Player 1's symbol ("X").
   • -1 represents Player 2's symbol ("O").

self.state = np.zeros(size, dtype=np.float)

2. Player Turns: Players alternate turns, with the current player represented by self.player.

self.player = 1  # Player 1 starts

3. Move Validation: The move(loc) method ensures only valid moves are allowed, updating the game state if successful.

def move(self, loc):
    i, j = loc
    if self.state[i, j] == 0:
        self.state[i, j] = self.player
        return True
    return False

4. Victory Detection: The get_score() method checks whether a player has won, leveraging the get_lines and in_a_row functions.

def get_score(self):
    i, j = self.last_move
    hor, ver, diag_right, diag_left = get_lines(self.state, (i, j))
    for line in [ver, hor, diag_right, diag_left]:
        if in_a_row(line, self.N, self.player):
            return self.player
    return None

5. Available Moves: The available_moves() function identifies all unoccupied cells, critical for generating legal actions during gameplay.

def available_moves(self):
    indices = np.moveaxis(np.indices(self.state.shape), 0, -1)
    return indices[self.state == 0]

Key Functions Explained

get_lines(matrix, loc)

This function extracts four "lines" passing through a specific grid location:

1. Horizontal line (entire row of the cell)
2. Vertical line (entire column of the cell)
3. Right diagonal (top-left to bottom-right)
4. Left diagonal (top-right to bottom-left)

def get_lines(matrix, loc):
    i, j = loc
    hor = matrix[:, j]        # Horizontal line
    ver = matrix[i, :]        # Vertical line
    diag_right = ...          # Top-left to bottom-right
    diag_left = ...           # Top-right to bottom-left
    return hor, ver, diag_right, diag_left

in_a_row(v, N, i)

This helper function determines if a vector contains N consecutive symbols for a given player. For instance:

• Input: [0, 1, 1, 1, 0], N=3, i=1
• Output: True (Player 1 has 3 in a row)

def in_a_row(v, N, i):
    if len(v) < N:
        return False
    _, _, total = get_runs(v, i)
    return np.any(total >= N)

get_runs(v, i)

A utility to identify sequences of a player's symbol in a vector. It returns:

• Start indices of sequences.
• End indices of sequences.
• Lengths of sequences.

def get_runs(v, i):
    bounded = np.hstack(([0], (v == i).astype(int), [0]))
    difs = np.diff(bounded)
    starts, = np.where(difs > 0)
    ends, = np.where(difs < 0)
    return starts, ends, ends - starts

Why This Setup Works

This implementation captures the complexity of the game while remaining flexible for AI training. The use of NumPy ensures computational efficiency, which is critical when running thousands of simulations during Monte Carlo Tree Search (MCTS).

You can explore the full implementation of the ConnectN class in the repository here.

Next, we'll explore how MCTS works and how it integrates seamlessly with our custom game setup.

---

3. What is Monte Carlo Tree Search (MCTS)?

Monte Carlo Tree Search (MCTS) is a powerful algorithm that balances exploration and exploitation to make decisions in complex domains like games, simulations, and planning problems. It’s at the heart of AlphaZero’s success, allowing it to evaluate vast decision trees without exhaustive search. Let’s break down MCTS, its components, and how it integrates into our Tic-Tac-Toe AI.

---

Basics of MCTS

At its core, MCTS uses random simulations and statistical reasoning to navigate game trees. Unlike traditional minimax algorithms, which evaluate all possible game states, MCTS focuses computational resources on the most promising moves, making it efficient for large decision spaces.

MCTS operates in four key phases:

1. Selection

   • Starting from the root node, MCTS traverses the tree using a selection strategy, such as Upper Confidence Bound (UCB), which balances exploration (trying less-visited moves) and exploitation (choosing moves with higher win rates).
   • The formula for UCB is:
     
     Where:
     • Q(s, a): The average value of the node.
     • N_s: Total visits to the parent node.
     • n_sa: Total visits to the current node.
     • c: Exploration constant, controlling the balance between exploration and exploitation.

2. Expansion

   • Once an unvisited or underexplored node is found, MCTS adds a new child node to the tree, representing a potential move. This ensures the tree expands as needed, keeping the exploration dynamic and adaptive.

3. Simulation (Rollout)

   • A simulation is run from the newly added node, where moves are selected randomly or heuristically until a terminal state (win, loss, or draw) is reached. The outcome of this simulation is used to estimate the value of the node.

4. Backpropagation

   • The simulation’s result propagates back through the tree, updating the values (( Q )) of all nodes traversed. This allows the algorithm to refine its understanding of which moves are most advantageous.

---

Exploration vs. Exploitation Trade-off

The key challenge in MCTS is balancing:

• Exploration: Investigating less-visited nodes to discover potentially better moves.
• Exploitation: Leveraging known high-reward nodes to maximize immediate gain.

The UCB formula elegantly handles this trade-off by incorporating both the node's value and the uncertainty (visit count), guiding the search dynamically.

For a deep dive into the mathematics behind UCB and its role in MCTS, refer to this excellent explanation here.

---

How MCTS Works Step-by-Step

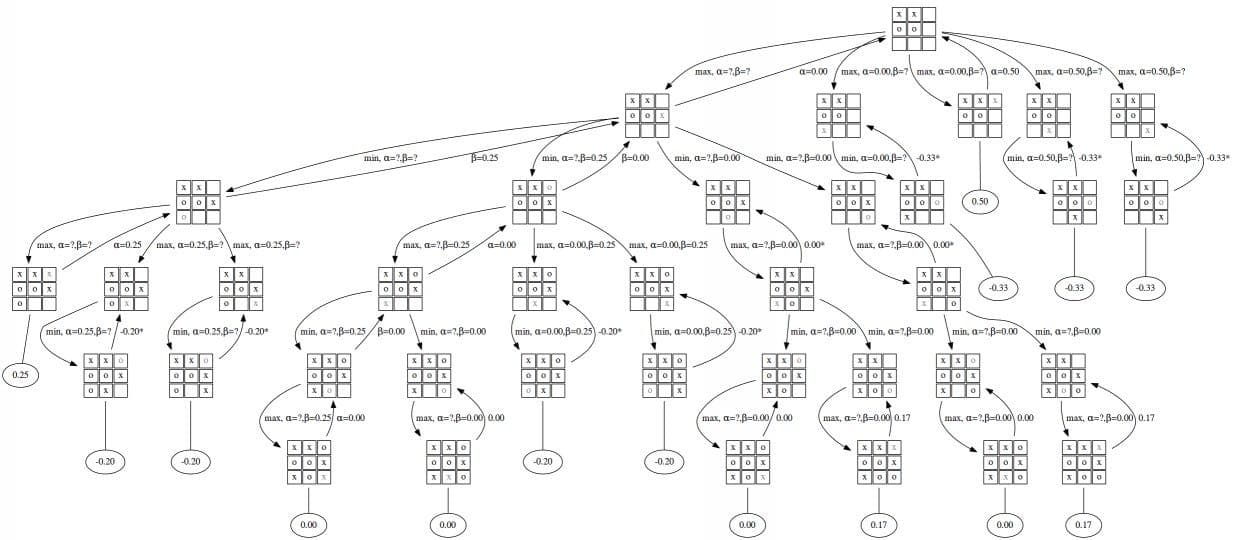
Let’s summarize how MCTS operates in a game like Tic-Tac-Toe:

1. Root Node Initialization:
   The game board's current state is represented as the root node of the tree.

2. Tree Traversal:
   The algorithm navigates the tree using UCB until it reaches a leaf node or an unexplored state.

3. Expansion and Rollout:
   A new child node is created for an unexplored move, followed by a simulation to a terminal state.

4. Result Evaluation:
   The outcome of the simulation (win, loss, or draw) is recorded.

5. Backpropagation:
   The simulation result is backpropagated, updating the visit count and value estimates for all nodes in the path.

6. Next Move Selection:
   Once the search completes (based on a preset number of iterations or time limit), the move with the highest visit count or value is selected.

---

Integration with AlphaZero

MCTS alone is powerful, but when combined with AlphaZero’s neural network, it becomes even more formidable. Here’s how the two work together:

1. Policy Guidance:
   AlphaZero’s neural network outputs a policy (probabilities of each move) and a value (expected game outcome) for any given board state. These guide the MCTS during simulation and rollout phases.

2. State Representation:
   The board state is fed into the neural network, which processes it and provides move probabilities. These probabilities replace uniform random rollouts, improving MCTS efficiency.

3. Rollout Optimization:
   Instead of running simulations to terminal states, AlphaZero’s MCTS leverages the neural network’s value function to estimate outcomes.

4. Training Loop:
   MCTS provides high-quality self-play data to train the neural network, creating a feedback loop where the AI improves iteratively by learning from its own games.

For a deeper dive into how MCTS integrates with AlphaZero, check out DeepMind’s paper on AlphaZero here.

---

Why MCTS for Tic-Tac-Toe?

Even though Tic-Tac-Toe is a smaller game compared to Chess or Go, MCTS provides several advantages:

• Efficiency: It avoids brute-force search, focusing only on promising moves.
• Scalability: The algorithm can scale up to larger games like Connect Four or Go.
• Adaptability: The balance between exploration and exploitation ensures robust decision-making in both small and complex game states.

---

In the next section, we’ll delve into building the neural network architecture that powers our AlphaZero-inspired agent, which integrates seamlessly with MCTS for optimal decision-making. Stay tuned!

4. Building the Neural Network for AlphaZero

The neural network is a crucial component of our AlphaZero-inspired Tic-Tac-Toe agent. It serves two key purposes: guiding the Monte Carlo Tree Search (MCTS) with policy probabilities and evaluating board states with value predictions. Let's break down the architecture, purpose, and functionality of the network, implemented as the Policy class.

You can get a refresher on how policy based methods works in Reinforcement Learning in this blog where I use Reinforcement Learning to train an agent to play hangman.

---

Overview of the Policy Network Architecture

The policy network is a convolutional neural network (CNN) designed to process the 6x6 game board. It outputs two essential predictions:

1. Policy (Action Head): Probabilities for all possible moves, guiding MCTS to focus on promising actions.
2. Value (Value Head): An evaluation of the board state, estimating the likelihood of the current player winning from this position.

Input Representation (Game State)

The board state is represented as a 6x6 grid with:

• 1: Indicates Player 1's move.
• -1: Indicates Player 2's move.
• 0: Represents an empty cell.

This input is reshaped into a format compatible with CNN layers and passed through the network.

---

The Architecture

import torch
import torch.nn as nn
import torch.nn.functional as F

class Policy(nn.Module):

    def __init__(self, game):
        super(Policy, self).__init__()

        # Input = 6x6 board
        # Convert to 5x5x16
        self.conv1 = nn.Conv2d(1, 16, kernel_size=2, stride=1, bias=False)
        # 5x5x16 to 3x3x32
        self.conv2 = nn.Conv2d(16, 32, kernel_size=3, stride=1, bias=False)

        self.size = 3 * 3 * 32
        
        # The part for actions (Policy Head)
        self.fc_action1 = nn.Linear(self.size, self.size // 4)
        self.fc_action2 = nn.Linear(self.size // 4, 36)
        
        # The part for the value function (Value Head)
        self.fc_value1 = nn.Linear(self.size, self.size // 6)
        self.fc_value2 = nn.Linear(self.size // 6, 1)
        self.tanh_value = nn.Tanh()
        
    def forward(self, x):
        # Convolutional layers
        y = F.leaky_relu(self.conv1(x))
        y = F.leaky_relu(self.conv2(y))
        y = y.view(-1, self.size)
        
        # Policy Head (Action probabilities)
        a = self.fc_action2(F.leaky_relu(self.fc_action1(y)))
        avail = (torch.abs(x.squeeze()) != 1).type(torch.FloatTensor)
        avail = avail.reshape(-1, 36)
        maxa = torch.max(a)
        exp = avail * torch.exp(a - maxa)
        prob = exp / torch.sum(exp)
        
        # Value Head (Board evaluation)
        value = self.tanh_value(self.fc_value2(F.leaky_relu(self.fc_value1(y))))
        return prob.view(6, 6), value

Key Components

1. Convolutional Layers:
   The network starts with two convolutional layers that process the game board:

   • The first layer reduces the 6x6 input to a 5x5x16 representation.
   • The second layer further reduces this to 3x3x32.

   These layers extract spatial features from the board, such as clusters of moves or potential winning lines.

2. Policy Head (Action Output):
   This branch predicts the probability distribution over all 36 possible moves:

   • Two fully connected layers transform the extracted features into probabilities for each cell.
   • The output is masked using avail, ensuring invalid moves (already occupied cells) receive zero probability.

   Output: A 6x6 grid of probabilities, guiding MCTS to prioritize promising actions.

3. Value Head (Game Outcome Prediction):
   This branch evaluates the board state, predicting the expected outcome of the game:

   • Two fully connected layers reduce the features to a single scalar value.
   • The output is passed through a tanh activation, ensuring it falls within the range [-1, 1]:
     • 1: Indicates a win for the current player.
     • -1: Indicates a loss.
     • 0: Suggests a likely draw.

4. Forward Pass:

   • The policy probabilities and value predictions are computed simultaneously.
   • The network outputs these predictions for use in MCTS:
     • Policy: Guides action selection during simulations.
     • Value: Provides state evaluation, reducing the need for random rollouts.

---

Why This Architecture?

1. Spatial Awareness:
   Convolutional layers efficiently extract patterns from the grid, identifying potential lines of victory or threat.

2. Parallel Outputs:
   Simultaneous computation of policy and value ensures the network is fast and suitable for iterative MCTS simulations.

3. Scalability:
   The modular design allows scaling to larger grids (e.g., 8x8 or 19x19) with minimal architectural changes.

---

In the next section, we’ll explore how this neural network integrates with MCTS to train a robust AlphaZero-inspired agent.

5. Training AlphaZero with MCTS

The training process combines Monte Carlo Tree Search (MCTS) and neural network optimization to iteratively improve the AlphaZero agent. In this section, we’ll explore how the training loop works, key stages such as MCTS simulation and backpropagation, and the parameters that govern the process.

---

Explanation of the Training Loop

The training loop is the heart of AlphaZero’s self-learning mechanism. It involves multiple games of self-play, where the agent plays against itself to generate high-quality data for improving the policy network.

1. MCTS Simulation for Move Selection

During each turn in a game:

• MCTS is used to explore possible moves and evaluate the board states resulting from those moves.
• The network’s policy output guides the MCTS by prioritizing likely good moves.
• The value head predicts the expected game outcome from any given board state, allowing MCTS to avoid full rollouts to terminal states.

The key steps in this phase are:

• Initializing a new MCTS tree (mytree).
• Iteratively running MCTS simulations up to a maximum number of iterations (Nmax).
• Selecting the next move based on MCTS results and temperature-controlled probabilities.

2. Backpropagation of Values

After a game is complete:

• The final outcome (win, loss, or draw) is used to compute the loss for the value head.
• The probabilities predicted by the policy network are compared to the improved move probabilities generated by MCTS.

Loss terms include:

• Policy Loss: Measures the divergence between the network’s predicted probabilities and the MCTS-guided probabilities.
• Value Loss: Measures the difference between the network’s predicted value and the actual game outcome.

These losses are aggregated and used to backpropagate gradients through the network.

3. Optimizing the Policy Network

The optimizer (Adam in this case) updates the network parameters using the computed gradients. The network learns to:

• Predict better move probabilities for MCTS.
• Provide more accurate value estimates for game states.

Optimization happens after every game of self-play, ensuring continuous improvement throughout training.

---

Key Parameters in Training

1. Number of Episodes

The training loop runs for a large number of episodes (50000 in this example). Each episode corresponds to one self-play game. The high number of episodes ensures:

• The network has sufficient data to generalize.
• MCTS benefits from exploring a wide variety of board states.

2. Exploration Constants (c and Nmax)

• c: Balances exploration and exploitation in MCTS using the Upper Confidence Bound (UCB) formula. A higher c value encourages more exploration.
• Nmax: Sets the maximum number of MCTS iterations per move, controlling the computational budget for each turn.

3. Learning Rate and Regularization

The optimizer uses a learning rate of 0.005 and a weight decay (1e-5) to ensure stable training and prevent overfitting.

---

Training Process Walkthrough

1. Initialize the Agent:

   • Create the game environment (ConnectN) and policy network (Policy).
   • Initialize the optimizer with Adam.

2. Self-Play Games:

   • Use MCTS to simulate games where the agent plays against itself.
   • Generate move probabilities and state evaluations.

3. Compute Loss:

   • Use the outcomes of the games to calculate:
     • Policy Loss: Encourages the network to predict MCTS-guided probabilities.
     • Value Loss: Ensures accurate game outcome predictions.

4. Optimize the Network:

   • Backpropagate the gradients through the policy network.
   • Update parameters to improve performance.

5. Save Checkpoints:

   • Save the trained model at regular intervals for evaluation and reuse.

---

Monitoring Training

Metrics:

• Policy Loss: Tracks the network’s ability to predict MCTS probabilities.
• Game Outcomes: Tracks the agent’s performance (win, loss, draw) over time.

Here is the training code snippet:

# initialize our alphazero agent and optimizer
import torch.optim as optim


game=ConnectN(**game_setting)
policy = Policy(game)
optimizer = optim.Adam(policy.parameters(), lr=.005, weight_decay=1.e-5)

# train our agent

from collections import deque
import MCTS

# try a higher number
episodes = 50000

import progressbar as pb
widget = ['training loop: ', pb.Percentage(), ' ', 
          pb.Bar(), ' ', pb.ETA() ]
timer = pb.ProgressBar(widgets=widget, maxval=episodes).start()

outcomes = []
policy_loss = []

Nmax = 2000

for e in range(1, episodes+1):

    mytree = MCTS.Node(game)
    logterm = []
    vterm = []
    
    while mytree.outcome is None:
        for _ in range(Nmax):
            mytree.explore(policy)
            if mytree.N >= Nmax:
                break
            
        current_player = mytree.game.player
        mytree, (v, nn_v, p, nn_p) = mytree.next()
        mytree.detach_mother()
        
        loglist = torch.log(nn_p)*p
        constant = torch.where(p>0, p*torch.log(p),torch.tensor(0.))
        logterm.append(-torch.sum(loglist-constant))

        vterm.append(nn_v*current_player)
        
    # we compute the "policy_loss" for computing gradient
    outcome = mytree.outcome
    outcomes.append(outcome)
    
    loss = torch.sum( (torch.stack(vterm)-outcome)**2 + torch.stack(logterm) )
    optimizer.zero_grad()
    loss.backward()
    policy_loss.append(float(loss))

    optimizer.step()
    
    if e%100==0:
        print("game: ",e+1, ", mean loss: {:3.2f}".format(np.mean(policy_loss[-20:])),
              ", recent outcomes: ", outcomes[-10:])
    
    if e%500==0:
        torch.save(policy,'6-6-4-pie-{:d}.policy'.format(e))
    del loss
    
    timer.update(e+1)
    
timer.finish()

---

Summary

The training loop allows AlphaZero to learn iteratively by playing against itself, leveraging MCTS to generate high-quality data. Through backpropagation, the network refines its understanding of optimal strategies and board evaluations, leading to an increasingly stronger AI.

In the next section, we’ll dive into the code walkthrough of the MCTS code, providing detailed insights into the implementation.

6. Code Walkthrough of Monte Carlo Tree Search

In this section, we’ll take a detailed look at the implementation of Monte Carlo Tree Search (MCTS) in the file MCTS.py. This script is the backbone of AlphaZero's decision-making process, guiding move selection based on self-play simulations.

---

Overview of MCTS in the Code

The MCTS implementation consists of several interconnected components:

1. Node Representation (Node class): Models the game tree, storing information about states, values, and visit counts.
2. Policy Integration (process_policy function): Uses the neural network to guide MCTS simulations.
3. Tree Exploration (explore method): Traverses and expands the game tree.
4. Move Selection (next method): Selects the next move based on the results of simulations.

---

Key Components of the Code

1. Node Representation (Node Class)

The Node class models each state in the game tree. It stores information such as:

• Game State (self.game): Represents the current board configuration.
• Child Nodes (self.child): Maps actions to subsequent game states.
• Visit Count (self.N): Tracks the number of times a node is visited.
• Value (self.V): Represents the expected outcome from this node.
• Probability (self.prob): Move probabilities from the neural network.

Key initialization highlights:

class Node:
    def __init__(self, game, mother=None, prob=torch.tensor(0., dtype=torch.float)):
        self.game = game
        self.child = {}
        self.U = 0
        self.prob = prob
        self.nn_v = torch.tensor(0., dtype=torch.float)
        self.N = 0
        self.V = 0
        self.outcome = self.game.score
        self.mother = mother

Game Outcomes: If the game has ended (win, loss, or draw), the node is initialized with the final result:

if self.game.score is not None:
    self.V = self.game.score * self.game.player
    self.U = 0 if self.game.score == 0 else self.V * float('inf')

2. Policy Integration (process_policy)

This function uses the neural network to guide MCTS by providing:

• Move Probabilities: Which moves are likely to be optimal.
• State Value (v): The expected outcome from the current state.

Key steps:

• Transformations: Rotates or flips the game board to improve generalization during training.
• Masking: Ensures only legal moves are assigned probabilities.
• Neural Network Prediction: Feeds the transformed board state into the network.

def process_policy(policy, game):
    frame = torch.tensor(game.state * game.player, dtype=torch.float, device=device)
    input = frame.unsqueeze(0).unsqueeze(0)
    prob, v = policy(input)
    mask = torch.tensor(game.available_mask(), device=device)
    available_moves = game.available_moves()
    probs = prob[mask == 1].view(-1)
    return available_moves, probs, v.squeeze().squeeze()

3. Tree Exploration (explore Method)

The explore method navigates the game tree using the Upper Confidence Bound (UCB) formula.

Key steps:

• Traverse Tree: Starts at the root and selects child nodes with the highest UCB values.
• Expand Tree: Adds new child nodes for unexplored moves.
• Update Values: Backpropagates results to update VVV and NNN for all visited nodes.

def explore(self, policy):
    current = self
    while current.child and current.outcome is None:
        max_U = max(c.U for c in current.child.values())
        actions = [a for a, c in current.child.items() if c.U == max_U]
        action = random.choice(actions)
        current = current.child[action]
    
    if not current.child and current.outcome is None:
        next_actions, probs, v = process_policy(policy, current.game)
        current.create_child(next_actions, probs)
        current.V = -float(v)
    current.N += 1

• Backpropagation: Updates values for all nodes in the path:

while current.mother:
    mother = current.mother
    mother.N += 1
    mother.V += (-current.V - mother.V) / mother.N
    for sibling in mother.child.values():
        sibling.U = sibling.V + c * float(sibling.prob) * sqrt(mother.N) / (1 + sibling.N)
    current = current.mother

4. Move Selection (next Method)

This method determines the next move after completing MCTS simulations. It selects moves based on the visit counts of child nodes, with a temperature parameter controlling exploration.

Key steps:

• Winning Moves: Prioritizes moves that guarantee a win.
• Probability Normalization: Converts visit counts to probabilities for move selection.

def next(self, temperature=1.0):
    if not self.child:
        raise ValueError('no children found and game hasn\'t ended')
    max_U = max(c.U for c in self.child.values())
    prob = torch.tensor([(node.N ** (1 / temperature)) for node in self.child.values()])
    prob /= torch.sum(prob)
    nextstate = random.choices(list(self.child.values()), weights=prob)[0]
    return nextstate, (-self.V, -self.nn_v, prob, prob)

Summary

The MCTS.py script provides a robust implementation of Monte Carlo Tree Search by:

1. Integrating neural network predictions for efficient search.
2. Balancing exploration and exploitation using UCB.
3. Dynamically expanding the game tree during self-play.

In the next section, we'll evaluate the AlphaZero agent and analyze its performance metrics.

7. Evaluating the AlphaZero Agent

After training, evaluating the AlphaZero-inspired agent is essential to measure its effectiveness and identify areas for improvement. This section explores the metrics used for evaluation, visualizing gameplay to assess strategy, and managing trained policies for future use.

---

Metrics for Evaluation

1. Win Rate Against Random Opponents

The win rate is a straightforward metric to evaluate the agent's performance:

• The trained agent competes against a random opponent that selects moves uniformly from the set of available actions.
• A high win rate indicates the agent has developed a robust strategy.

Key Implementation:

• The Challenge_Player_MCTS function uses the trained policy (challenge_policy) to guide MCTS simulations during gameplay.
• By testing the agent in multiple games, we compute the win rate as:

Win Rate = Games Won/Total Games Played

2. Training Loss Over Episodes

The loss during training provides insight into the agent's learning progress:

• Policy Loss: Measures how well the network’s predicted probabilities align with the MCTS-guided probabilities.
• Value Loss: Tracks the accuracy of game outcome predictions.

A steady decline in loss over episodes indicates effective training and convergence.

Visualizing Training Loss:
Plotting the loss values over time using libraries like matplotlib helps identify trends and potential overfitting.

import matplotlib.pyplot as plt

plt.plot(range(len(policy_loss)), policy_loss)
plt.xlabel('Episodes')
plt.ylabel('Loss')
plt.title('Training Loss Over Episodes')
plt.show()

Visualizing the Gameplay

Visualization is crucial to understanding the strategies developed by the agent:

• Simulated Gameplay: Using the Challenge_Player_MCTS function, the agent plays games against itself or a random opponent.
• Move-by-Move Visualization: Board states are displayed after each move to observe the agent's decision-making process.

Implementation: The Play class is used to orchestrate gameplay, where Challenge_Player_MCTS makes decisions for Player 1. Enabling %matplotlib notebook allows dynamic visualization.

%matplotlib notebook

gameplay = Play(
    ConnectN(**game_setting), 
    player1=Challenge_Player_MCTS, 
    player2=None
)

This setup visualizes:

• Move Sequences: The evolution of the board state during the game.
• Winning Strategies: Patterns such as prioritizing blocking the opponent or creating multiple threats.

Here's how it looks like when you play on a jupyter notebook.

And here's how it will look like after we have finished building our app in the third part of the series. But more on that later.

Summary

Evaluating the AlphaZero agent involves:

1. Measuring its win rate against random opponents to gauge strategic strength.
2. Analyzing training loss trends to ensure convergence and learning effectiveness.
3. Visualizing gameplay to observe and interpret the agent's strategies.
4. Managing trained policies by saving and loading them for reproducibility and future development.

In the next section, we'll discuss challenges encountered during implementation, lessons learned, and potential enhancements to improve the agent further.

8. Challenges and Considerations

Building an AlphaZero-inspired agent for Tic-Tac-Toe is an exciting journey, but it comes with its own set of challenges. While the simplified environment of Tic-Tac-Toe serves as a learning playground, several nuances in implementation and strategy need to be addressed. In this section, we'll discuss the key challenges faced, limitations of the current approach, and lessons learned during development.

---

Key Challenges in Implementing AlphaZero for Tic-Tac-Toe

Even though this agent is impossible to win against if you take second turn, and pretty challenging if you move first (this game has a first mover's advantage), it's not without its challenges.

1. Adapting AlphaZero for a Small Game  

AlphaZero was originally designed for complex games like Chess and Go. Scaling it down for a smaller game like Tic-Tac-Toe required several modifications:

• Exploration Constants (c): Balancing exploration and exploitation with an appropriate exploration constant was challenging in a small state space.

• Neural Network Design: Designing a lightweight neural network for Tic-Tac-Toe, without overfitting to the limited number of unique board states, was a critical consideration.

2. MCTS Computational Overhead  

Monte Carlo Tree Search, while powerful, is computationally expensive:

• Simulations per Move: Running thousands of simulations per move for a relatively simple game can be overkill, leading to unnecessary resource consumption.

• Balancing Simulations and Training: Optimizing the number of MCTS iterations (Nmax) while maintaining training efficiency was a delicate trade-off.

3. Handling Symmetries  

The Tic-Tac-Toe board has inherent symmetries (rotations and reflections). Leveraging these symmetries for better generalization required:

• Implementing transformations in MCTS.py to augment training data.

• Ensuring that these transformations did not introduce errors during backpropagation or policy inference.

---

Limitations of the Current Approach

While the implementation works well for a 6x6 Tic-Tac-Toe game, there are notable limitations:

1. Simplified Neural Network  

The policy network is intentionally small to suit the low complexity of Tic-Tac-Toe. However, this simplicity limits its ability to generalize to more complex games or state spaces.

2. Scalability  

The current implementation is designed for a small-scale game. Extending this to larger board sizes (e.g., Connect Four or Go) would require:

• A deeper and more sophisticated neural network.

• Efficient memory management for MCTS simulations over larger state spaces.

3. Training Data Sparsity  

Even with self-play, the relatively small number of unique board configurations in Tic-Tac-Toe can lead to:

• Limited training diversity.

• Overfitting to specific strategies or board states.

4. Fixed Exploration Constant (c)  

The exploration constant remains static throughout training. A more dynamic adjustment of c could better adapt to the agent's learning progress and the complexity of board states.

---

Lessons Learned During Development

1. Simplicity First  

Starting with a small game like Tic-Tac-Toe helped me focus on core concepts such as:

• Efficient integration of MCTS with a neural network.

• Proper backpropagation of value and policy losses.

This foundation can later be scaled to more complex environments.

2. The Power of Self-Play  

Self-play proved invaluable in teaching the agent optimal strategies without external input:

• The agent developed nuanced tactics, such as blocking the opponent while simultaneously building its own threats.

• Self-play also highlighted the importance of balancing exploration and exploitation during training.

3. Importance of Visualization  

Visualizing gameplay was instrumental in:

• Debugging issues in MCTS simulations and move selection.

• Understanding the strategies developed by the agent.

• Identifying cases where the agent made suboptimal decisions, guiding further improvements.

4. Resource Management Matters  

Monte Carlo Tree Search can become a computational bottleneck if not tuned properly. Setting reasonable limits for:

• Number of simulations per move (Nmax).

• Number of training episodes.

Helped achieve a balance between resource usage and training efficiency.

---

Summary

Implementing AlphaZero for Tic-Tac-Toe was both a challenging and enlightening experience. While the game's simplicity allowed rapid iterations, it also highlighted key limitations such as computational overhead and scalability challenges. However, the lessons learned---particularly about the integration of MCTS and neural networks---lay a strong foundation for tackling more complex games in the future.

In the next and final section of this blog, we'll summarize our achievements, preview the next steps in this series, and discuss how you can build on this work to create even smarter agents.

9. Conclusion and Next Steps

Recap of Achievements in This Part

In this first part of our journey to build an AlphaZero-inspired Tic-Tac-Toe agent, we’ve laid a solid foundation by covering:

1. Understanding AlphaZero’s Power:
   We explored how AlphaZero revolutionized AI in strategy games through a combination of Monte Carlo Tree Search (MCTS) and self-play reinforcement learning.

2. Customizing Tic-Tac-Toe:
   We adapted the classic game to a more challenging 6x6 grid with a 4-in-a-row winning condition, setting the stage for developing a robust AI agent.

3. Integrating Neural Networks with MCTS:
   The neural network’s policy head provided move probabilities, while the value head estimated the game outcome, enabling MCTS to make smarter decisions efficiently.

4. Training with MCTS and Self-Play:
   Through iterative self-play and backpropagation, we trained the agent to improve its strategy, showcasing the power of reinforcement learning.

5. Evaluation and Challenges:
   We evaluated the agent’s performance using win rates, visualized its gameplay, and reflected on challenges and limitations, such as balancing computational efficiency and model scalability.

This part has equipped us with a fully functional, trained AlphaZero-style agent that excels at 6x6 Tic-Tac-Toe. But what good is a powerful AI without an interface for others to interact with it?

---

Preview of the Next Blog: Developing a FastAPI Backend

In the next part of this series, we’ll bring our Alpha Zero AI to life by developing a robust backend using FastAPI. Here’s what you can look forward to:

• Building RESTful Endpoints: We’ll create APIs for starting a game, making moves, and getting AI recommendations.
• Integrating the Trained Model: The backend will use our trained AlphaZero agent to play Tic-Tac-Toe dynamically.
• Real-Time Performance: Leveraging FastAPI’s asynchronous capabilities, we’ll ensure the backend is fast, responsive, and scalable.

This backend will serve as the bridge between our AI and a user-friendly frontend, which we’ll tackle in Part 3 of the Alpha Zero with MCTS series.

---

Codes: Check the Github Repo for the full code

Happy Coding!

🔙 Back to all blogs | 🏠 Home Page

---

About the Author

Sagarnil Das

Sagarnil Das is a seasoned AI enthusiast with over 12 years of experience in Machine Learning and Deep Learning.

He has built scalable AI ecosystems for global giants like the NHS and developed innovative mental health applications that detect emotions and suicidal tendencies.

Some of his other accomplishments includes:

• Ex-NASA researcher
• Ex-Udacity Mentor
• Intel Edge AI scholarship winner
• Kaggle Notebooks expert

When he's not immersed in data or crafting AI models, Sagarnil enjoys playing the guitar and doing street photography.

An avid Dream Theater fan, he believes in blending logic with creativity to solve complex problems.

You can find out more about Sagarnil here.

To contact him regarding any guidance, questions, feedbacks or challenges, you can contact him by clicking the chat icon on the bottom right of the screen.

Connect with Sagarnil: