AI-Powered Diagonal Sudoku Solver with Constraint Propagation

Table of Contents

1. Introduction

    - What is Sudoku?

    - Why Diagonal Sudoku?

    - Why Build an AI for Sudoku?

2. Project Overview

    - Objectives

    - Key Features

3. Understanding Constraint Propagation

    - What is Constraint Propagation?

    - Role in Sudoku Solving

4. Implementing the Naked Twins Strategy

    - What are Naked Twins?

    - Algorithm Explanation

    - Code Implementation

5. Handling Diagonal Constraints

    - Defining Diagonal Sudoku

    - Integrating Diagonals into the Solver

    - Code Implementation

6. Code Structure and Explanation

    - Overview of solution.py

    - Key Functions and Their Roles

    - Understanding unitlist, units, and peers

7. Visualization of the Solver

    - Using Pygame for Visualization

    - Running the Visualization

    - Interpreting the Visualization Output

8. Conclusion

    - Recap of Key Concepts

    - Potential Enhancements

    - Final Thoughts

---

1 - Introduction

Welcome to an in-depth exploration of building an AI-powered Diagonal Sudoku Solver using Constraint Propagation techniques.

In this blog, I will guide you through the entire development process, from setting up your development environment to implementing and optimizing the solver.

Whether you're an aspiring artificial intelligence enthusiast or a seasoned programmer looking to enhance your problem-solving skills, this comprehensive guide is designed to provide you with valuable insights and practical code examples to create an efficient Sudoku-solving AI.

The complete code for this project is available here: AI Sudoku Github Repository

1.1 What is Sudoku?

Sudoku is a widely popular number-placement puzzle that challenges players to fill a 9x9 grid so that each column, each row, and each of the nine 3x3 subgrids (also known as "boxes" or "regions") contain all of the digits from 1 to 9 exactly once. The puzzle starts with a partially filled grid, and the objective is to complete the grid following these constraints.

For a comprehensive overview of Sudoku, you can visit the Wikipedia page on Sudoku.

Here's a simple illustration of a standard Sudoku puzzle:

5 3 _ | _ 7 _ | _ _ _
6 _ _ | 1 9 5 | _ _ _
_ 9 8 | _ _ _ | _ 6 _
------+-------+------
8 _ _ | _ 6 _ | _ _ 3
4 _ _ | 8 _ 3 | _ _ 1
7 _ _ | _ 2 _ | _ _ 6
------+-------+------
_ 6 _ | _ _ _ | 2 8 _
_ _ _ | 4 1 9 | _ _ 5
_ _ _ | _ 8 _ | _ 7 9

In this grid:

• Rows: Each of the nine horizontal lines must contain all digits from 1 to 9 without repetition.
• Columns: Each of the nine vertical lines must also contain all digits from 1 to 9 without repetition.
• Subgrids: Each of the nine 3x3 subgrids must contain all digits from 1 to 9 without repetition.

Sudoku puzzles range in difficulty based on the number of initially filled cells and the strategies required to solve them.

While simple puzzles can be solved with basic elimination techniques, more complex ones may require advanced strategies like Naked Twins, Hidden Pairs, and Constraint Propagation.

For an in-depth explanation of these strategies, refer to Sudoku Dragon's strategy guide.

1.2 Why Build an AI for Sudoku?

Developing an AI to solve Sudoku puzzles may appear straightforward at first glance, but it encompasses a range of computational and algorithmic challenges that make it an excellent project for honing artificial intelligence and algorithm design skills. Here's why building a Sudoku-solving AI is beneficial:

• Understanding Constraint Propagation: Sudoku is inherently a constraint satisfaction problem. Building an AI to solve it helps in understanding how to model and solve such problems efficiently.

• Algorithm Design and Optimization: Implementing strategies like Naked Twins and Diagonal Constraints requires careful algorithm design to ensure that the solver is both accurate and efficient.

• Enhancing Problem-Solving Skills: Tackling the complexities of Sudoku-solving algorithms sharpens logical reasoning and problem-solving abilities, which are crucial in various AI applications.

• Practical Application of AI Concepts: This project provides a hands-on opportunity to apply AI concepts such as search algorithms, backtracking, and optimization in a tangible and engaging way.

• Scalability and Extensibility: While the project focuses on Diagonal Sudoku, the underlying principles can be extended to other constraint satisfaction problems, making the skills acquired highly transferable.

Moreover, Sudoku serves as a microcosm for many real-world applications where constraint satisfaction and optimization are key, such as scheduling, resource allocation, and puzzle-solving in robotics. For more on constraint satisfaction problems, visit the Wikipedia page on Constraint Satisfaction Problems.

---

2 - Project Overview

---

2.1 Objectives

The primary objective of this project is to develop an AI-powered Diagonal Sudoku Solver that can efficiently solve complex Sudoku puzzles by leveraging advanced constraint propagation techniques. Specifically, the project aims to achieve the following:

• Automate Sudoku Solving: Create a solver that can automatically solve both standard and diagonal Sudoku puzzles without manual intervention.

• Implement Advanced Strategies: Incorporate strategies such as Naked Twins and Diagonal Constraints to enhance the solver's capability to handle more challenging puzzles.

• Optimize Performance: Ensure that the solver operates efficiently, minimizing computation time and maximizing accuracy through optimized algorithms.

2.2 Key Features

The Diagonal Sudoku Solver boasts a range of features designed to provide both functionality and educational value:

• Constraint Propagation Techniques: Utilizes methods like Elimination, Only Choice, and Naked Twins to systematically reduce the number of possible solutions, streamlining the solving process.

• Diagonal Constraints Integration: Extends traditional Sudoku rules by adding diagonal constraints, ensuring that both main diagonals contain all digits from 1 to 9 exactly once.

• Efficient Algorithm Design: Implements a combination of depth-first search and backtracking algorithms to explore possible number assignments effectively, ensuring the solver can handle puzzles of varying difficulty levels.

For a detailed overview of the solver's capabilities, refer to the Wikipedia page on Sudoku Solving Algorithms.

---

3 - Understanding Constraint Propagation

---

Constraint Propagation is a fundamental technique in artificial intelligence used to reduce the search space by enforcing constraints throughout the problem-solving process.

In the context of Sudoku, constraint propagation involves iteratively applying rules to eliminate possible numbers from cells based on the current state of the grid.

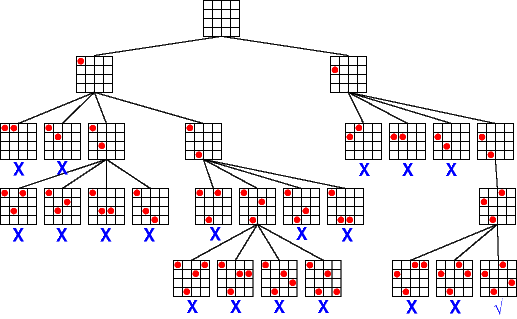
Key AI strategies employed in building the Sudoku solver include:

• Elimination: Removing numbers from the list of possible candidates for a cell based on the numbers already present in its row, column, and subgrid.

• Only Choice: Assigning a number to a cell if that number can only fit in one possible cell within a row, column, or subgrid.

• Naked Twins: Identifying pairs of cells within a unit (row, column, or subgrid) that contain the same two possible numbers. These numbers can then be eliminated from the list of possible candidates for the other cells in the unit. Learn more about the Naked Twins strategy here.

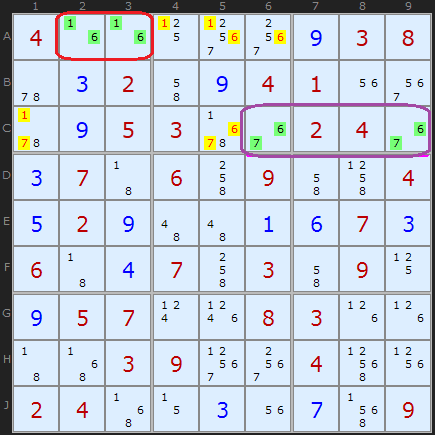
• Diagonal Constraints: Extending the standard Sudoku rules by adding constraints along the two main diagonals, ensuring that each diagonal also contains all digits from 1 to 9 exactly once.

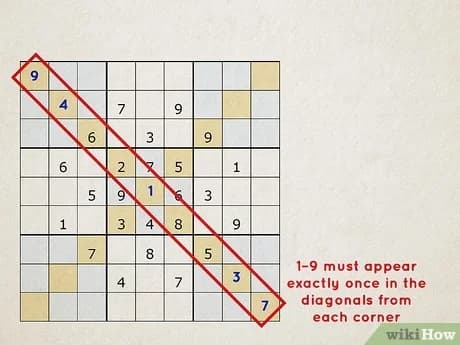
• Search Algorithms: Implementing depth-first search combined with backtracking to explore possible number assignments systematically until a valid solution is found. For an introduction to search algorithms in AI, check out the GeeksforGeeks search algorithms overview.

By integrating these strategies, the AI becomes capable of solving even the most challenging Sudoku puzzles efficiently. This project not only demonstrates the practical application of AI techniques but also provides a solid foundation for tackling more complex constraint satisfaction and optimization problems in the future.

---

4 - Implementing the Naked Twins Strategy

---

4.1 What are Naked Twins?

When I delved deeper into enhancing the Sudoku solver, I encountered the Naked Twins strategy—a powerful technique that significantly improves the solver's efficiency. But what exactly are Naked Twins?

Naked Twins occur when two cells within the same unit (a row, column, or 3x3 subgrid) contain the exact same pair of possible digits, and only those two digits. This scenario implies that these two digits must occupy those two cells, allowing us to eliminate those digits from the remaining cells in the same unit. By doing so, we reduce the number of possible candidates for other cells, streamlining the solving process.

Example Illustration:

Imagine a row in a Sudoku puzzle where two cells have the possible digits '23' and '23', respectively. These are Naked Twins. Since these two digits must occupy these two cells, we can confidently remove '2' and '3' from the list of possible digits for all other cells in that row.

Here's a visual representation:

Row: [ '23', '23', '1', '4', '5', '6', '7', '8', '9' ]

After applying the Naked Twins strategy, the row remains unchanged except that '2' and '3' are removed from the other cells (if they were present).

For a more detailed explanation and additional examples, you can refer to the Sudoku Dragon Strategy Guide.

4.2 Algorithm Explanation

Implementing the Naked Twins strategy involves several thoughtful steps to ensure that we accurately identify and eliminate the appropriate digits. Here's how I approached it:

1. Identify Potential Naked Twins:

   • Iterate Through Each Unit: For every unit (row, column, or subgrid), I looked for cells that have exactly two possible digits.
   • Find Matching Pairs: Among these cells, I searched for pairs that share the same two digits. These pairs are the Naked Twins.

2. Eliminate Twin Digits from Peers:

   • Traverse the Unit: Once a pair of Naked Twins is identified, I went through each cell in the same unit.
   • Remove Twin Digits: For cells that are not part of the Naked Twins, I removed the twin digits from their list of possible values. This elimination narrows down the possibilities, making it easier to solve those cells.

3. Repeat the Process:

   • Multiple Iterations: Since identifying Naked Twins can open up new opportunities for elimination, the algorithm continues to iterate through all units until no more eliminations can be made using this strategy.

Why It Works:

The Naked Twins strategy leverages the fundamental principles of constraint propagation. By recognizing that certain digits must occupy specific cells, we can confidently eliminate those digits from other cells within the same unit, reducing the complexity of the puzzle.

For those interested in the theoretical underpinnings of this strategy, the Wikipedia page on Constraint Satisfaction Problems offers a comprehensive overview of how such techniques are applied in various domains.

4.3 Code Implementation

Translating the Naked Twins strategy into code was both challenging and rewarding. Here's how I implemented it in Python:

import itertools

def naked_twins(values):
    """
    Eliminate values using the naked twins strategy.
    See link for details: http://www.sudokudragon.com/sudokustrategy.htm
    Args:
        values(dict): a dictionary of the form {'box_name': '123456789', ...}
    Returns:
        The values dictionary with the naked twins eliminated from peers.
    """
    for unit in unitlist:
        # Step 1: Find all boxes with two possible digits
        pairs = [box for box in unit if len(values[box]) == 2]
        
        # Step 2: Find all possible pairs of these boxes
        poss_twins = list(itertools.combinations(pairs, 2))
        
        for pair in poss_twins:
            box1, box2 = pair
            # Step 3: Check if the pair forms naked twins
            if values[box1] == values[box2]:
                twin_digits = values[box1]
                # Step 4: Eliminate the twin digits from other boxes in the unit
                for box in unit:
                    if box != box1 and box != box2:
                        for digit in twin_digits:
                            values[box] = values[box].replace(digit, '')
    return values

Breakdown of the Code:

1. Iterating Through Units:

   • The function begins by iterating through each unit in the unitlist. This list contains all rows, columns, subgrids, and diagonal units.

2. Identifying Potential Twins:

   • For each unit, it first identifies all boxes that have exactly two possible digits (len(values[box]) == 2).
   • It then generates all possible pairs of these boxes using itertools.combinations.

3. Validating Naked Twins:

   • For each pair, it checks if both boxes contain the exact same two digits. If they do, these boxes are recognized as Naked Twins.

4. Eliminating Twin Digits from Other Boxes:

   • Once Naked Twins are identified, the algorithm iterates through all other boxes in the same unit.
   • It removes the twin digits from the list of possible values for these boxes, effectively narrowing down their possibilities.

Example in Action:

Suppose within a row, two boxes are identified with the values '23' and '23'. These are Naked Twins. The algorithm will then remove '2' and '3' from the possible values of all other boxes in that row.

Visual Representation:

To further illustrate the effectiveness of the Naked Twins strategy, let's consider a more dynamic example where the elimination of digits from other cells in the unit leads to a significant reduction in possibilities.

Initial State:

Imagine a row in a Sudoku puzzle with the following possible values for each cell:

Row: [ '23', '23', '1', '245', '5', '6', '7', '8', '9' ]

• Cell 1: '23'
• Cell 2: '23'
• Cell 3: '1'
• Cell 4: '245'
• Cell 5: '5'
• Cell 6: '6'
• Cell 7: '7'
• Cell 8: '8'
• Cell 9: '9'

In this scenario:

• Cells 1 and 2 are Naked Twins because they both contain the exact same pair of possible digits: '2' and '3'.
• These twins indicate that the digits '2' and '3' must occupy Cell 1 and Cell 2 in some order.

Applying the Naked Twins Strategy:

Since '2' and '3' are confined to Cells 1 and 2, we can eliminate these digits from the possible values of all other cells in the same row. Specifically, we target Cell 4, which initially has the possible digits '245'.

Elimination Process:

• Cell 4: '245' → After eliminating '2' and '3', the possible digits reduce to '45'.

Resulting State:

Row: [ '23', '23', '1', '45', '5', '6', '7', '8', '9' ]

• Cell 4 now has fewer possibilities: '45' instead of '245'.

Visual Representation Before and After Applying Naked Twins:

Cell	Before Naked Twins	After Naked Twins
1	23	23
2	23	23
3	1	1
4	245	45
5	5	5
6	6	6
7	7	7
8	8	8
9	9	9

Impact of Naked Twins:

By identifying and applying the Naked Twins strategy, we've successfully reduced the possible digits for Cell 4 from '245' to '45'. This reduction not only simplifies the solving process for Cell 4 but also enhances the overall efficiency of the solver by narrowing down the search space.

Why This Matters:

Implementing the Naked Twins strategy in this manner demonstrates how constraint propagation can effectively streamline the solving process. Each elimination step brings the solver closer to the final solution by methodically reducing the number of possible candidates for each cell.

For more intricate examples and a deeper understanding of how Naked Twins can be leveraged in various units (rows, columns, and subgrids), refer to the Sudoku Dragon Strategy Guide.

---

5 - Handling Diagonal Constraints

---

5.1 Defining Diagonal Sudoku

As I continued developing the Sudoku solver, I decided to take on the challenge of solving Diagonal Sudoku—a variation that adds an extra layer of complexity to the traditional puzzle. But what exactly is Diagonal Sudoku?

Diagonal Sudoku adheres to all the standard Sudoku rules: each row, each column, and each of the nine 3x3 subgrids must contain all digits from 1 to 9 exactly once. Additionally, it introduces two new constraints:

• Main Diagonals: Both of the main diagonals (from the top-left to the bottom-right and from the top-right to the bottom-left) must also contain all digits from 1 to 9 exactly once.

This means that in addition to the usual constraints, the solver must ensure that the numbers 1 through 9 appear without repetition along both diagonals. Incorporating these diagonal constraints significantly increases the solver's complexity and showcases the power of constraint propagation in handling more intricate rules.

For a comprehensive understanding of Diagonal Sudoku, you can refer to the Wikipedia page on Sudoku Variants, which details various modifications and their unique challenges.

5.2 Integrating Diagonals into the Solver

Integrating diagonal constraints into the Sudoku solver was an exciting part of the project. I approached this by treating the diagonals as additional units, similar to rows, columns, and subgrids. Here's how I implemented it:

1. Defining Diagonal Units:

   • I created two new lists representing the two main diagonals of the Sudoku grid.
   • Each diagonal is treated as a separate unit, ensuring that the digits 1 through 9 appear exactly once along each diagonal.

2. Updating the Unit List:

   • I extended the existing unitlist by adding these two diagonal units.
   • This inclusion allows the solver to apply constraint propagation techniques not just within rows, columns, and subgrids, but also along the diagonals.

3. Adjusting Peers and Units:

   • By updating the units and peers dictionaries to account for the new diagonal units, the solver can now recognize and enforce the additional constraints.
   • This ensures that any assignment of a digit along a diagonal is properly propagated to eliminate that digit from other cells in the same diagonal.

This integration was pivotal in enabling the solver to handle Diagonal Sudoku effectively. It demonstrated how versatile the constraint propagation approach is, allowing for the seamless addition of new rules without overhauling the existing architecture.

For more insights into handling additional constraints in Sudoku, the Sudoku Dragon Strategy Guide offers valuable strategies and examples.

5.3 Code Implementation

Translating the concept of Diagonal Sudoku into code was a straightforward yet crucial step. Here's how I implemented the diagonal constraints within the solver:

import itertools

def cross(A, B):
    "Cross product of elements in A and elements in B."
    return [s+t for s in A for t in B]

rows = 'ABCDEFGHI'
cols = '123456789'

boxes = cross(rows, cols)

row_units = [cross(r, cols) for r in rows]
column_units = [cross(rows, c) for c in cols]
square_units = [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')]

# Define the two main diagonals
diag_units = [
    [rows[i] + cols[i] for i in range(9)],
    [rows[::-1][i] + cols[i] for i in range(9)]
]

# Combine all units including the diagonals
unitlist = row_units + column_units + square_units + diag_units

# Create a dictionary mapping each box to its units
units = {s: [u for u in unitlist if s in u] for s in boxes}

# Create a dictionary mapping each box to its peers
peers = {s: set(sum(units[s], [])) - {s} for s in boxes}

Breakdown of the Implementation:

1. Defining Diagonal Units:

   • I created two lists within diag_units:
     • The first list captures the top-left to bottom-right diagonal.
     • The second list captures the top-right to bottom-left diagonal.

2. Updating the Unit List:

   • By appending diag_units to the existing unitlist, I ensured that the solver treats diagonals as additional units.
   • This allows all constraint propagation strategies to consider diagonal constraints alongside traditional Sudoku rules.

3. Mapping Units and Peers:

   • The units dictionary maps each box to all the units it belongs to, including diagonals.
   • The peers dictionary defines all the boxes that share a unit with a given box, ensuring that constraints are properly enforced across all relevant cells.

Visual Representation of Diagonal Constraints Integration:

Before adding diagonals:

Units: [Rows, Columns, Subgrids]

After adding diagonals:

Units: [Rows, Columns, Subgrids, Diagonals]

This simple yet effective addition transforms the solver from handling standard Sudoku puzzles to tackling the more complex Diagonal Sudoku variations.

---

6 - Code Structure and Explanation

---

6.1 Overview of solution.py

The core of the solver resides in the solution.py file, which houses all the necessary functions and data structures to parse, solve, and display Sudoku puzzles. This modular approach not only enhances readability but also facilitates easier maintenance and potential future expansions.

Key Components of solution.py:

• Helper Functions: Functions like cross and assign_value aid in generating combinations and managing value assignments within the Sudoku grid.

• Data Structures: Definitions for rows, columns, boxes, units, and peers form the backbone of the solver's logic, enabling it to navigate and apply constraints effectively.

• Solving Strategies: Implementation of strategies such as Elimination, Only Choice, Naked Twins, and Constraint Propagation empower the solver to tackle both standard and Diagonal Sudoku puzzles with ease.

• Search Algorithms: Incorporation of depth-first search and backtracking algorithms ensures that the solver can explore possible solutions systematically until it finds a valid one.

• Visualization: While optional, integrating visualization tools like Pygame offers a dynamic way to observe the solver in action, enhancing the user experience.

6.2 Key Functions and Their Roles

Understanding the primary functions within solution.py is crucial to grasping how the Sudoku solver operates. Here's a breakdown of the most significant functions and their responsibilities:

1. cross(A, B)

   • Purpose: Generates the cross product of elements in A and B, effectively creating combinations of rows and columns to identify individual boxes (e.g., 'A1', 'B3').

   • Usage Example:

     rows = 'ABCDEFGHI'
     cols = '123456789'
     boxes = cross(rows, cols)  # Generates ['A1', 'A2', ..., 'I9']
     

2. assign_value(values, box, value)

   • Purpose: Assigns a value to a specific box within the Sudoku grid and records this assignment if the box is solved (i.e., contains a single digit). This function is pivotal for tracking changes and facilitating visualization.

   • Usage Example:

     values = assign_value(values, 'A1', '5')
     

3. naked_twins(values)

   • Purpose: Implements the Naked Twins strategy by identifying pairs of boxes within the same unit that have identical pairs of possible digits. It then eliminates these digits from the remaining boxes in that unit, thereby reducing the search space.

   • Usage Example:

     values = naked_twins(values)
     

4. grid_values(grid)

   • Purpose: Converts a string representation of a Sudoku grid into a dictionary format, where each box maps to its possible digits. Empty cells are represented by the string '123456789', indicating all possible digits are initially valid.

   • Usage Example:

     grid = '2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3'
     values = grid_values(grid)
     

5. display(values)

   • Purpose: Prints the Sudoku grid in a human-readable 2-D format, allowing users to visualize the current state of the puzzle.

   • Usage Example:

     display(values)
     

6. eliminate(values)

   • Purpose: Applies the Elimination strategy by removing known digits from the list of possible values for each peer of every solved box. This reduction is essential for narrowing down potential candidates.

   • Usage Example:

     values = eliminate(values)
     

7. only_choice(values)

   • Purpose: Implements the Only Choice strategy by assigning a digit to a box if that digit can only fit in one box within a unit. This ensures that digits are placed correctly based on uniqueness within their respective units.

   • Usage Example:

     values = only_choice(values)
     

8. single_possibility(values)

   • Purpose: Assigns a digit to a box if it is the only possible digit that can occupy that box after eliminating digits based on solved peers. Although not the most efficient strategy, it complements other methods by handling straightforward assignments.

   • Usage Example:

     values = single_possibility(values)
     

9. reduce_puzzle(values)

   • Purpose: Iteratively applies the Elimination and Only Choice strategies until no further progress can be made. It also includes sanity checks to ensure that the puzzle remains solvable at each step.

   • Usage Example:

     values = reduce_puzzle(values)
     

10. search(values)

    • Purpose: Utilizes depth-first search combined with constraint propagation to explore possible digit assignments systematically. It recursively attempts assignments and backtracks upon encountering invalid states until a solution is found or all possibilities are exhausted.

    • Usage Example:

      solved = search(values)
      

11. solve(grid)

    • Purpose: Serves as the main function to solve a Sudoku puzzle. It converts the input grid into a dictionary, initiates the solving process, and returns the solved grid if a solution exists.

    • Usage Example:

      solution = solve(grid)
      

Each of these functions collaborates seamlessly to ensure that the Sudoku solver operates efficiently and accurately. By combining elimination techniques with strategic searching, the solver can handle both standard and Diagonal Sudoku puzzles with ease.

6.3 Understanding unitlist, units, and peers

At the heart of the Sudoku solver lie three critical data structures: unitlist, units, and peers. These structures define the relationships and constraints within the Sudoku grid, enabling the solver to apply constraint propagation effectively.

1. unitlist

   • Definition: A list of all units within the Sudoku grid. A unit is a collection of boxes that must contain all digits from 1 to 9 exactly once. In standard Sudoku, units include rows, columns, and 3x3 subgrids. For Diagonal Sudoku, the two main diagonals are also treated as units.

   • Construction:

     unitlist = row_units + column_units + square_units + diag_units
     

   • Components:

     • row_units: Each row of the grid.
     • column_units: Each column of the grid.
     • square_units: Each 3x3 subgrid.
     • diag_units: The two main diagonals.

2. units

   • Definition: A dictionary mapping each box to a list of all units that contain that box. This association allows the solver to quickly identify all constraints applicable to a particular box.

   • Construction:

     units = {s: [u for u in unitlist if s in u] for s in boxes}
     

   • Usage Example:

     units['A1']  # Might return [row_units[0], column_units[0], square_units[0], diag_units[0]]
     

3. peers

   • Definition: A dictionary mapping each box to a set of all its peers. Peers are boxes that share a common unit with the given box. This includes all boxes in the same row, column, subgrid, and, for Diagonal Sudoku, the diagonals.

   • Construction:

     peers = {s: set(sum(units[s], [])) - {s} for s in boxes}
     

   • Explanation:

     • sum(units[s], []): Flattens the list of units for box s into a single list.
     • set(...) - {s}: Converts the list to a set and removes the box itself, leaving only its peers.

   • Usage Example:

     peers['A1']  # Might return {'A2', 'A3', ..., 'B1', 'C1', ..., 'B2', 'C3', ...}
     

Visual Representation:

Consider the box E5 in the Sudoku grid:

• Units Containing E5:

  • Row Unit: All boxes in row E (E1 to E9).
  • Column Unit: All boxes in column 5 (A5 to I5).
  • Square Unit: All boxes in the central 3x3 subgrid (D4 to F6).
  • Diagonal Units: Both main diagonals if E5 lies on them.

• Peers of E5:

  • Row Peers: E1, E2, E3, E4, E6, E7, E8, E9
  • Column Peers: A5, B5, C5, D5, F5, G5, H5, I5
  • Square Peers: D4, D5, D6, E4, E6, F4, F5, F6
  • Diagonal Peers (if applicable): Depending on the grid's configuration.

By defining unitlist, units, and peers in this manner, the solver gains a comprehensive understanding of the Sudoku grid's constraints. This setup is crucial for effectively applying constraint propagation techniques like Elimination, Only Choice, and Naked Twins, ensuring that the solver can systematically narrow down possibilities and arrive at a valid solution.

Final Thoughts:

The meticulous construction of unitlist, units, and peers underscores the importance of robust data structures in AI-driven problem-solving. By accurately mapping the relationships and constraints within the Sudoku grid, the solver is empowered to apply intelligent strategies that mirror human logical reasoning. This foundational setup not only enhances the solver's efficiency but also exemplifies the seamless integration of algorithmic design with practical AI applications.

For a more detailed exploration of these concepts, you might find the Wikipedia page on Constraint Satisfaction Problems insightful.

Here's the full code

import itertools


def cross(A, B):
    "Cross product of elements in A and elements in B."
    return [s+t for s in A for t in B]

rows = 'ABCDEFGHI'
cols = '123456789'

boxes = cross(rows, cols)

row_units = [cross(r, cols) for r in rows]
column_units = [cross(rows, c) for c in cols]
square_units = [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')]
diag_units = [[rows[i] + cols[i] for i in range(9)], [rows[::-1][i] + cols[i] for i in range(9)]]
unitlist = row_units + column_units + square_units + diag_units
units = dict((s, [u for u in unitlist if s in u]) for s in boxes)
peers = dict((s, set(sum(units[s],[]))-set([s])) for s in boxes)

assignments = []


def assign_value(values, box, value):
    """
    Please use this function to update your values dictionary!
    Assigns a value to a given box. If it updates the board record it.
    """
    values[box] = value
    if len(value) == 1:
        assignments.append(values.copy())
    return values


def naked_twins(values):
    """
    Eliminate values using the naked twins strategy.
    See link for details: http://www.sudokudragon.com/sudokustrategy.htm
    Args:
        values(dict): a dictionary of the form {'box_name': '123456789', ...}
    Returns:
        The values dictionary with the naked twins eliminated from peers.
    """
    # Naked twins: two boxes in same unit that have a pair of identical digits
    # remaining as their only possibilities
    for unit in unitlist:
        # Find all boxes with two digits remaining as possibilities
        pairs = [box for box in unit if len(values[box]) == 2]
        # Pairwise combinations
        poss_twins = [list(pair) for pair in itertools.combinations(pairs, 2)]
        for pair in poss_twins:
            box1 = pair[0]
            box2 = pair[1]
            # Find the naked twins
            if values[box1] == values[box2]:
                for box in unit:
                    # Eliminate the naked twins as possibilities for peers
                    if box != box1 and box != box2:
                        for digit in values[box1]:
                            values[box] = values[box].replace(digit,'')
    return values


def grid_values(grid):
    """
    Convert grid into a dict of {square: char} with '123456789' for empties.
    Args:
        grid(string) - A grid in string form.
    Returns:
        A grid in dictionary form
            Keys: The boxes, e.g., 'A1'
            Values: The value in each box, e.g., '8'. If the box has no value, then the value will be '123456789'.
    """
    chars = []
    digits = '123456789'
    for c in grid:
        if c in digits:
            chars.append(c)
        if c == '.':
            chars.append(digits)
    # Nine by nine grid
    assert len(chars) == 81
    return dict(zip(boxes, chars))


def display(values):
    """
    Display the values as a 2-D grid.
    Args:
        values(dict): The sudoku in dictionary form
    """
    width = 1+max(len(values[s]) for s in boxes)
    line = '+'.join(['-'*(width*3)]*3)
    for r in rows:
        print(''.join(values[r+c].center(width)+('|' if c in '36' else '')
                      for c in cols))
        if r in 'CF': print(line)
    print


def eliminate(values):
    """
    Go through all the boxes, and whenever there is a box with a value, eliminate this value from the values of all its peers.
    Args:
        A sudoku in dictionary form.
    Returns:
        The resulting sudoku in dictionary form.
    """
    solved_values = [box for box in values.keys() if len(values[box]) == 1]
    for box in solved_values:
        digit = values[box]
        # Remove solved digit from the list of possible values for each peer
        for peer in peers[box]:
            values[peer] = values[peer].replace(digit,'')
    return values


def only_choice(values):
    """
    Go through all the units, and whenever there is a unit with a value that only fits in one box, assign the value to this box.
    Args:
        A sudoku in dictionary form.
    Returns:
        The resulting sudoku in dictionary form.
    """
    for unit in unitlist:
        for digit in '123456789':
            # Create a list of all the boxes in the unit in question
            # that contain the digit in question
            dplaces = [box for box in unit if digit in values[box]]
            if len(dplaces) == 1:
                # This box is the only choice for this digit
                values = assign_value(values, dplaces[0], digit)
    return values


def single_possibility(values):
    """
    Assign values using the single possibility strategy.
    See link for details: http://www.sudokudragon.com/sudokustrategy.htm
    This strategy is not very sophisticated, which is reflected in its poor performance time-wise (often ~190x slower than the only_choice assignment strategy).
    Args:
        values(dict): a dictionary of the form {'box_name': '123456789', ...}
    Returns:
        The values dictionary with squares assigned their only possible value.
    """
    for box in boxes:
        digits = '123456789'
        for digit in digits:
            for peer in peers[box]:
                # Remove solved peers from digit possibilities
                if len(values[peer]) == 1:
                    digits = digits.replace(values[peer],'')
        # Only one digit can go in this box i.e. a single possibility
        if len(digits) == 1:
            values = assign_value(values, box, digits)
    return values


def reduce_puzzle(values):
    """
    Iterate eliminate() and only_choice(). If at some point, there is a box with no available values, return False.
    If the sudoku is solved, return the sudoku.
    If after an iteration of both functions, the sudoku remains the same, return the sudoku.
    Args:
        A sudoku in dictionary form.
    Returns:
        The resulting sudoku in dictionary form.
    """
    stalled = False
    while not stalled:
        solved_values_before = len([box for box in values.keys() if len(values[box]) == 1])
        # Apply the eliminate exclusion strategy
        values = eliminate(values)
        # Apply the only choice assignment strategy
        values = only_choice(values)
        solved_values_after = len([box for box in values.keys() if len(values[box]) == 1])
        # Stop applying these strategies if we stop making box-solving progress
        stalled = solved_values_before == solved_values_after
        # Sanity check: never eliminate all digits from a box's possibilities
        if len([box for box in values.keys() if len(values[box]) == 0]):
            return False
    return values


def search(values):
    """
    Using depth-first search and propagation, try all possible values.
    Args:
        A sudoku in dictionary form.
    Returns:
        The solved sudoku if solvable or False if not solvable.
    """
    # First, reduce the puzzle using the previous function
    values = reduce_puzzle(values)
    if values is False:
        return False  # Failed earlier
    if all(len(values[s]) == 1 for s in boxes):
        return values  # Solved!
    # Choose one of the unfilled squares with the fewest possibilities
    n,s = min((len(values[s]), s) for s in boxes if len(values[s]) > 1)
    # Now use recurrence to solve each one of the resulting sudokus,
    # and if one returns a value (not False), return that answer!
    for value in values[s]:
        new_sudoku = values.copy()
        new_sudoku[s] = value
        attempt = search(new_sudoku)
        if attempt:
            return attempt


def solve(grid):
    """
    Find the solution to a Sudoku grid.
    Args:
        grid(string): a string representing a sudoku grid.
            Example: '2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3'
    Returns:
        The dictionary representation of the final sudoku grid. False if no solution exists.
    """
    # Convert string grid to dictionary grid
    values = grid_values(grid)
    solved = search(values)
    if solved:
        return solved
    else:
        return False

solve('2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3')

if __name__ == '__main__':
    diag_sudoku_grid = '2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3'
    display(solve(diag_sudoku_grid))

    try:
        from visualize import visualize_assignments
        visualize_assignments(assignments)

    except SystemExit:
        pass
    except:
        print('We could not visualize your board due to a pygame issue. Not a problem! It is not a requirement.')

---

7. Visualization of the Solver

7.1 Using Pygame for Visualization

The Sudoku solver includes a visualization feature powered by Pygame. This module provides a graphical representation of the Sudoku board as the solver iterates through its solution process. Here's how the visualization works:

• The play function in the PySudoku module displays the Sudoku board.
• Each frame of the solving process is drawn dynamically, showing the progressive elimination of possibilities in each cell.
• A pre-designed Sudoku board image (sudoku-board-bare.jpg) is used as the background for the visualization.

The play function iterates through the solution states stored in the assignments list, dynamically updating the displayed board to show the solver's progress. Additionally, solved cells are displayed with their final values, making it easy to follow the solver's logic.

7.2 Running the Visualization

Here's a video of the sudoku getting solved with Constraint Satisfaction method using Naked Queens strategy, Depth First Search and Backtracking.

1. Setup: Ensure you have all required files in your working directory:

   • The solution.py script containing the solver.
   • The PySudoku module for visualization.
   • The Sudoku board image (sudoku-board-bare.jpg).

2. Execute the Solver:

   • Run the solution.py script. If you've configured the visualize_assignments function, the solver will store all intermediate states in the assignments list.
   • When the solution is complete, the play function will use Pygame to display these states sequentially.

3. Saving a Video (Optional):

   • The modified play function now includes functionality to capture frames of the solving process and save them as a video file using the imageio library.
   • The output video (sudoku_solution.mp4 by default) will show the entire solving process, from the initial board setup to the final solution.

7.3 Interpreting the Visualization Output

The visualization is designed to make the solver's logic clear and accessible:

1. Initial Setup:

   • The unsolved Sudoku puzzle is displayed on the Pygame window, with empty cells represented as blank spaces.

2. Progression:

   • As the solver progresses, intermediate states are visualized. For example:
     • Cells that are solved are filled with their determined values.
     • Remaining cells show potential values being narrowed down through strategies like elimination and only-choice.

3. Completion:

   • When the solver finishes, the Sudoku board is fully solved, with all cells displaying their final values.
   • If the optional video-saving feature is enabled, the final video will end with the solved board.

This visualization is particularly helpful for:

• Debugging the solver to ensure it is functioning correctly.
• Understanding the step-by-step process of solving Sudoku puzzles using constraint propagation techniques.
• Demonstrating the solver's logic in an engaging and interactive way.

---

8. Conclusion

8.1 Recap of Key Concepts

This project demonstrates how an AI-driven Sudoku solver can solve puzzles using advanced constraint propagation techniques and a systematic search approach. Here's a recap of the key concepts covered:

1. Sudoku Representation:

   • The Sudoku board was represented as a dictionary, where each key corresponds to a cell (e.g., 'A1'), and the values represent the potential digits for that cell.
   • The grid was parsed from a string input, making it easy to define puzzles programmatically.

2. Constraint Propagation:

   • Elimination: Removed impossible values from peers of solved cells.
   • Only Choice: Assigned digits to cells when a digit could only fit in one location within a unit.
   • Naked Twins: Identified and eliminated pairs of digits confined to two boxes in the same unit.

3. Search and Backtracking:

   • The solver used a depth-first search strategy to explore possible solutions when constraint propagation alone could not solve the puzzle.
   • Backtracking ensured that incorrect paths were discarded systematically, leading to an optimized solution.

4. Visualization:

   • The solving process was visualized using Pygame, showing the board updates dynamically.
   • The terminal output logged the AI's thought process, providing insights into its reasoning.
   • The solving process was recorded as a video for review and sharing.

8.2 Potential Enhancements

While the current implementation is robust and functional, there is always room for improvement. Here are some potential enhancements:

1. Performance Optimization:

   • Implement more advanced constraint propagation strategies, such as "Hidden Pairs" or "X-Wing" to reduce reliance on search.
   • Use heuristic-based search algorithms to prioritize branches that are more likely to lead to solutions.

2. Enhanced Visualization:

   • Add animations to highlight cells being updated during constraint propagation.
   • Display probabilities or reasoning for specific moves visually on the board. For an example of probability-based reasoning, see this article on constraint solving.

3. User Interaction:

   • Allow users to input their own Sudoku puzzles through a graphical interface. Learn how to build GUIs in Python using Tkinter.
   • Add a feature to pause, step through, or replay the solving process. See an example of replayable visualizations.

4. Machine Learning Integration:

   • Train a neural network to predict potential solutions for cells, reducing reliance on rule-based techniques. A good starting point is this tutorial on deep learning for Sudoku.
   • Use reinforcement learning to develop an agent that learns Sudoku-solving strategies dynamically.

5. Support for More Variants:

   • Extend the solver to handle Sudoku variants like diagonal Sudoku (already partially supported), Samurai Sudoku, or Killer Sudoku. Learn about Sudoku variants.

6. Web or Mobile Application:

   • Deploy the solver as a web or mobile app to make it accessible to a broader audience, integrating visualization and logging features for educational purposes. Check out Flask for web apps and React Native for mobile apps.

8.3 Final Thoughts

This project illustrates the power of AI and algorithmic thinking in solving complex puzzles like Sudoku. The combination of constraint propagation, systematic search, and dynamic visualization bridges the gap between algorithmic rigor and user-friendly presentation.

By introducing deliberate delays and syncing the terminal output with the visualization, the solver becomes an engaging educational tool, offering insights into the problem-solving process. With further refinements and integrations, this solver could evolve into a powerful tool for teaching AI concepts, entertaining users, and solving more advanced puzzles.

We hope this project inspires further exploration and enhancements. Happy puzzling!

Explore the Project

Ready to dive deeper? Access the complete source code, detailed documentation, and ongoing updates on our GitHub repository. Whether you're looking to experiment with the AI, contribute to its development, or adapt it for your unique applications, the repository is your gateway to the Sudoku world.

Check out the Sudoku GitHub Repository

Thank you for following along! We hope this project has enriched your understanding of Constraint Propagation and inspired you to embark on your own AI adventures. Feel free to reach out with questions, feedback, or contributions---let's continue building intelligent systems together.

---

Happy Coding!

🔙 Back to all blogs | 🏠 Home Page

---

About the Author

Sagarnil Das

Sagarnil Das is a seasoned AI enthusiast with over 12 years of experience in Machine Learning and Deep Learning.

He has built scalable AI ecosystems for global giants like the NHS and developed innovative mental health applications that detect emotions and suicidal tendencies.

Some of his other accomplishments includes:

• Ex-NASA researcher
• Ex-Udacity Mentor
• Intel Edge AI scholarship winner
• Kaggle Notebooks expert

When he's not immersed in data or crafting AI models, Sagarnil enjoys playing the guitar and doing street photography.

An avid Dream Theater fan, he believes in blending logic with creativity to solve complex problems.

You can find out more about Sagarnil here.

To contact him regarding any guidance, questions, feedbacks or challenges, you can contact him by clicking the chat icon on the bottom right of the screen.

Connect with Sagarnil: